statistics — 數學統計函式

在 3.4 版本加入。

原始碼: Lib/statistics.py

---

此模組提供了用於計算數值型（Real 值）資料的數學統計量的函式。

此模組並非旨在與 NumPy、SciPy 等第三方庫，或 Minitab、SAS 和 Matlab 等面向專業統計學家的專有全功能統計軟體包競爭。它的目標是圖形計算器和科學計算器的級別。

除非明確指出，這些函式支援 int、float、Decimal 和 Fraction。目前不支援其他型別（無論是否在數值型別層次結構中）的行為。混合型別的集合也未定義且取決於具體實現。如果您的輸入資料包含混合型別，您可以使用 map() 來確保一致的結果，例如：map(float, input_data)。

一些資料集使用 NaN（非數字）值來表示缺失資料。由於 NaN 具有不尋常的比較語義，它們會在對資料進行排序或計數發生的統計函式中導致令人驚訝或未定義的行為。受影響的函式包括 median()、median_low()、median_high()、median_grouped()、mode()、multimode() 和 quantiles()。NaN 值應在呼叫這些函式之前進行剝離。

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

平均值和中心位置度量

這些函式計算總體或樣本的平均值或典型值。

mean()	資料的算術平均值（“平均數”）。
fmean()	快速浮點算術平均值，可選加權。
geometric_mean()	資料的幾何平均值。
harmonic_mean()	資料的調和平均值。
kde()	估計資料的機率密度分佈。
kde_random()	從 kde() 生成的 PDF 中進行隨機抽樣。
median()	資料的中位數（中間值）。
median_low()	資料的低中位數。
median_high()	資料的高中位數。
median_grouped()	分組資料的中位數（第 50 百分位數）。
mode()	離散或名義資料的單一眾數（最常見值）。
multimode()	離散或名義資料的眾數列表（最常見值）。
quantiles()	將資料分成等機率區間。

離散度度量

這些函式計算總體或樣本偏離典型值或平均值的程度。

pstdev()	資料的總體標準差。
pvariance()	資料的總體方差。
stdev()	資料的樣本標準差。
variance()	資料的樣本方差。

兩個輸入之間關係的統計量

這些函式計算兩個輸入之間關係的統計量。

covariance()	兩個變數的樣本協方差。
correlation()	皮爾遜和斯皮爾曼相關係數。
linear_regression()	簡單線性迴歸的斜率和截距。

函式詳情

注意：這些函式不要求傳入的資料已排序。然而，為了閱讀方便，大多數示例都展示了排序後的序列。

statistics.mean(data)

返回 data 的樣本算術平均值，data 可以是序列或可迭代物件。

算術平均值是資料之和除以資料點數量。它通常被稱為“平均值”，儘管它是許多不同數學平均值中的一種。它是資料中心位置的度量。

如果 data 為空，將引發 StatisticsError。

一些使用示例

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

備註

平均值受異常值影響很大，不一定是資料點的典型示例。對於更穩健（儘管效率較低）的中心趨勢度量，請參見 median()。

樣本均值提供了真實總體均值的無偏估計，因此在所有可能的樣本上取平均值時，mean(sample) 將收斂於整個總體的真實均值。如果 data 表示整個總體而不是樣本，則 mean(data) 等同於計算真實總體均值 μ。

statistics.fmean(data, weights=None)

將 data 轉換為浮點數並計算算術平均值。

這比 mean() 函式執行得更快，並且它總是返回一個 float。data 可以是序列或可迭代物件。如果輸入資料集為空，則會引發 StatisticsError。

>>> fmean([3.5, 4.0, 5.25])
4.25

支援可選加權。例如，一位教授透過將測驗權重設為 20%，作業權重設為 20%，期中考試權重設為 30%，期末考試權重設為 30% 來評定課程成績。

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

如果提供了 weights，它的長度必須與 data 相同，否則將引發 ValueError。

在 3.8 版本加入。

3.11 版本中的更改: 添加了對 weights 的支援。

statistics.geometric_mean(data)

將 data 轉換為浮點數並計算幾何平均值。

幾何平均值使用值的乘積（與使用值的總和的算術平均值相反）來表示 data 的中心趨勢或典型值。

如果輸入資料集為空、包含零或包含負值，則會引發 StatisticsError。data 可以是序列或可迭代物件。

未採取特殊措施以獲得精確結果。（然而，未來可能會改變。）

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

在 3.8 版本加入。

statistics.harmonic_mean(data, weights=None)

返回 data 的調和平均值，data 是實數值的序列或可迭代物件。如果省略 weights 或為 None，則假定為等權重。

調和平均值是資料倒數算術 mean() 的倒數。例如，三個值 a、b 和 c 的調和平均值將等同於 3/(1/a + 1/b + 1/c)。如果其中一個值為零，結果將為零。

調和平均值是一種平均值，是資料中心位置的度量。它通常適用於平均比率或速率，例如速度。

假設一輛車以 40 公里/小時的速度行駛 10 公里，然後以 60 公里/小時的速度行駛另外 10 公里。平均速度是多少？

>>> harmonic_mean([40, 60])
48.0

假設一輛車以 40 公里/小時的速度行駛 5 公里，然後交通疏導後，以 60 公里/小時的速度行駛剩餘的 30 公里。平均速度是多少？

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

如果 data 為空，任何元素小於零，或者加權和不為正，則引發 StatisticsError。

當前演算法在輸入中遇到零時會提前退出。這意味著後續輸入不會進行有效性檢查。（此行為未來可能會改變。）

在 3.6 版本加入。

3.10 版本中的更改: 添加了對 weights 的支援。

statistics.kde(data, h, kernel='normal', *, cumulative=False)

核密度估計 (KDE)：從離散樣本建立連續機率密度函式或累積分佈函式。

基本思想是使用核函式對資料進行平滑處理，以幫助從樣本中推斷總體。

平滑程度由稱為頻寬的縮放參數 h 控制。較小的值強調區域性特徵，而較大的值產生更平滑的結果。

kernel 決定了樣本資料點的相對權重。通常，核形狀的選擇不如影響力更大的頻寬平滑引數重要。

對每個樣本點都給予一定權重的核包括 normal (gauss)、logistic 和 sigmoid。

僅對頻寬內的樣本點給予權重的核包括 rectangular (uniform)、triangular、parabolic (epanechnikov)、quartic (biweight)、triweight 和 cosine。

如果 cumulative 為真，將返回一個累積分佈函式。

如果 data 序列為空，將引發 StatisticsError。

維基百科有一個示例，我們可以使用 kde() 從少量樣本中生成並繪製估計的機率密度函式。

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> f_hat = kde(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [f_hat(x) for x in xarr]

xarr 和 yarr 中的點可用於製作 PDF 圖。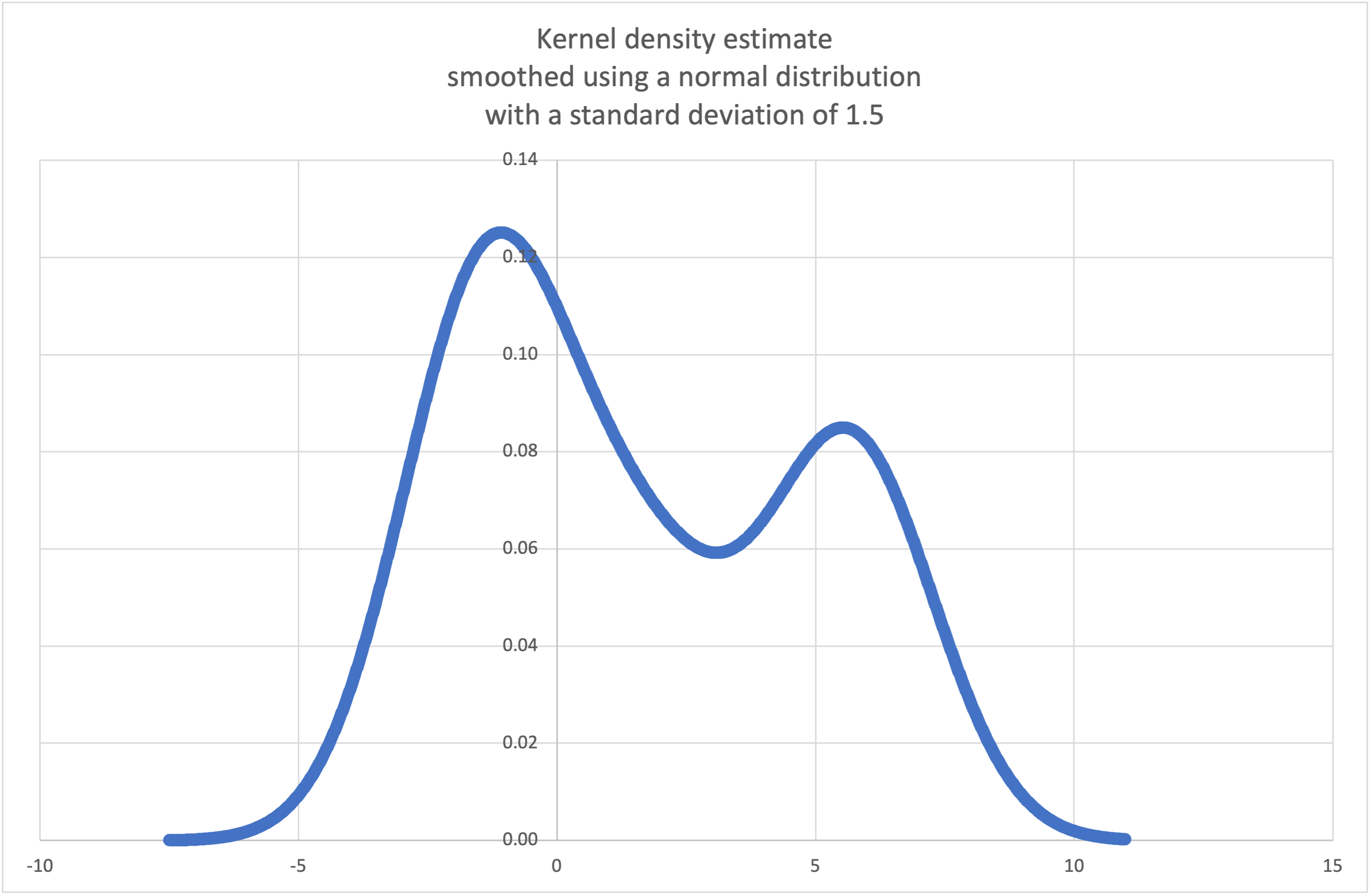

在 3.13 版本加入。

statistics.kde_random(data, h, kernel='normal', *, seed=None)

返回一個函式，該函式從 kde(data, h, kernel) 產生的估計機率密度函式中進行隨機選擇。

提供 seed 允許可重現的選擇。將來，隨著更精確的核逆 CDF 估計的實現，這些值可能會略有變化。seed 可以是整數、浮點數、字串或位元組。

如果 data 序列為空，將引發 StatisticsError。

繼續 kde() 的示例，我們可以使用 kde_random() 從估計的機率密度函式中生成新的隨機選擇。

>>> data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> rand = kde_random(data, h=1.5, seed=8675309)
>>> new_selections = [rand() for i in range(10)]
>>> [round(x, 1) for x in new_selections]
[0.7, 6.2, 1.2, 6.9, 7.0, 1.8, 2.5, -0.5, -1.8, 5.6]

在 3.13 版本加入。

statistics.median(data)

使用常見的“中間兩個值的平均值”方法，返回數值資料的中位數（中間值）。如果 data 為空，則引發 StatisticsError。data 可以是序列或可迭代物件。

中位數是衡量中心位置的穩健指標，受異常值影響較小。當資料點數量為奇數時，返回中間資料點。

>>> median([1, 3, 5])
3

當資料點數量為偶數時，透過取中間兩個值的平均值來插值中位數。

>>> median([1, 3, 5, 7])
4.0

這適用於您的資料是離散的，並且您不介意中位數可能不是實際資料點的情況。

如果資料是序數（支援排序操作）但不是數值（不支援加法），請考慮使用 median_low() 或 median_high()。

statistics.median_low(data)

返回數值資料的低中位數。如果 data 為空，則引發 StatisticsError。data 可以是序列或可迭代物件。

低中位數始終是資料集的成員。當資料點數量為奇數時，返回中間值。當資料點數量為偶數時，返回兩個中間值中較小的一個。

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

當您的資料是離散的並且您希望中位數是實際資料點而不是插值時，請使用低中位數。

statistics.median_high(data)

返回資料的高中位數。如果 data 為空，則引發 StatisticsError。data 可以是序列或可迭代物件。

高中位數始終是資料集的成員。當資料點數量為奇數時，返回中間值。當資料點數量為偶數時，返回兩個中間值中較大的一個。

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

當您的資料是離散的並且您希望中位數是實際資料點而不是插值時，請使用高中位數。

statistics.median_grouped(data, interval=1.0)

估計已分組或分箱在連續固定寬度區間中點附近的數值資料的中位數。

data 可以是任何可迭代的數值資料，其中每個值都恰好是箱子的中點。必須至少存在一個值。

interval 是每個箱子的寬度。

例如，人口統計資訊可能已被彙總為連續的十年年齡組，每個年齡組由區間的 5 年中點表示。

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

第 50 百分位數（中位數）是 1071 名成員佇列中的第 536 人。該人處於 30 至 40 歲年齡組。

常規的 median() 函式會假定三十多歲年齡組中的每個人都正好是 35 歲。一個更站得住腳的假設是該年齡組的 484 名成員均勻分佈在 30 歲到 40 歲之間。為此，我們使用 median_grouped()。

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

呼叫者有責任確保資料點以 interval 的精確倍數分隔。這對於獲得正確結果至關重要。該函式不檢查此前提條件。

輸入可以是任何可在插值步驟中強制轉換為浮點數的數值型別。

statistics.mode(data)

從離散或名義 data 中返回單個最常見的資料點。眾數（如果存在）是最典型的值，並作為中心位置的度量。

如果有多個具有相同頻率的眾數，則返回在 data 中遇到的第一個。如果需要其中最小或最大的眾數，請使用 min(multimode(data)) 或 max(multimode(data))。如果輸入 data 為空，則引發 StatisticsError。

mode 假定離散資料並返回單個值。這是眾數的標準處理方法，通常在學校教授。

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

眾數是此包中唯一一個也適用於名義（非數值）資料的統計量。

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

僅支援可雜湊輸入。要處理 set 型別，請考慮轉換為 frozenset。要處理 list 型別，請考慮轉換為 tuple。對於混合或巢狀輸入，請考慮使用這種較慢的二次演算法，它只依賴於相等性測試：max(data, key=data.count)。

3.8 版本中的更改: 現在透過返回遇到的第一個眾數來處理多眾數資料集。以前，當找到多個眾數時，它會引發 StatisticsError。

statistics.multimode(data)

返回 data 中出現頻率最高的值列表，按它們在 data 中首次出現的順序排列。如果存在多個眾數，將返回多個結果；如果 data 為空，則返回空列表。

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

在 3.8 版本加入。

statistics.pstdev(data, mu=None)

返回總體標準差（總體方差的平方根）。有關引數和其他詳細資訊，請參見 pvariance()。

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

返回 data 的總體方差，data 是一個非空序列或實數值的可迭代物件。方差，或關於均值的二階矩，是資料變異性（分散或離散）的度量。大方差表示資料分散，小方差表示資料緊密聚集在均值附近。

如果給定可選的第二個引數 mu，它應該是 data 的總體均值。它也可以用於計算不是均值的點的二階矩。如果它缺失或為 None（預設），則自動計算算術平均值。

使用此函式計算整個總體的方差。要從樣本估計方差，variance() 函式通常是更好的選擇。

如果 data 為空，則引發 StatisticsError。

示例：

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

如果您已經計算了資料的均值，可以將其作為可選的第二個引數 mu 傳入，以避免重新計算。

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

支援 Decimal 和 Fraction 型別。

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

備註

當對整個總體呼叫時，這給出總體方差 σ²。當對樣本呼叫時，這是有偏的樣本方差 s²，也稱為具有 N 自由度的方差。

如果您以某種方式知道真實的總體均值 μ，您可以使用此函式計算樣本的方差，將已知的總體均值作為第二個引數。假設資料點是總體的隨機樣本，結果將是總體方差的無偏估計。

statistics.stdev(data, xbar=None)

返回樣本標準差（樣本方差的平方根）。有關引數和其他詳細資訊，請參見 variance()。

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

返回 data 的樣本方差，data 是一個包含至少兩個實數值的可迭代物件。方差，或關於均值的二階矩，是資料變異性（分散或離散）的度量。大方差表示資料分散；小方差表示資料緊密聚集在均值附近。

如果給定可選的第二個引數 xbar，它應該是 data 的樣本均值。如果它缺失或為 None（預設），則自動計算均值。

當您的資料是總體的一個樣本時，請使用此函式。要計算整個總體的方差，請參見 pvariance()。

如果 data 的值少於兩個，則引發 StatisticsError。

示例：

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

如果您已經計算了資料的樣本均值，可以將其作為可選的第二個引數 xbar 傳入，以避免重新計算。

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

此函式不會嘗試驗證您是否將實際均值作為 xbar 傳入。對 xbar 使用任意值可能導致無效或不可能的結果。

支援 Decimal 和 Fraction 值。

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

備註

這是帶有貝塞爾校正的樣本方差 s²，也稱為具有 N-1 自由度的方差。假設資料點具有代表性（例如獨立同分布），結果應該是真實總體方差的無偏估計。

如果您以某種方式知道實際總體均值 μ，您應該將其作為 mu 引數傳遞給 pvariance() 函式以獲取樣本的方差。

statistics.quantiles(data, *, n=4, method='exclusive')

將 data 分成 n 個等機率的連續區間。返回一個由 n - 1 個分隔這些區間的切點組成的列表。

將 n 設定為 4 表示四分位數（預設）。將 n 設定為 10 表示十分位數。將 n 設定為 100 表示百分位數，它提供 99 個切點，將 data 分成 100 個大小相等的組。如果 n 不小於 1，則引發 StatisticsError。

data 可以是包含樣本資料的任何可迭代物件。為了獲得有意義的結果，data 中的資料點數量應大於 n。如果至少沒有一個數據點，則引發 StatisticsError。

切點是從最近的兩個資料點進行線性插值的。例如，如果一個切點落在兩個樣本值 100 和 112 之間距離的三分之一處，則切點將計算為 104。

計算分位數的 method 可以根據 data 是否包含或排除總體中最低和最高可能值而有所不同。

預設 method 為“exclusive”，用於從可能包含比樣本中發現的更極端值的總體中取樣的資料。低於 m 個排序資料點中的第 i 個的總體部分計算為 i / (m + 1)。給定九個樣本值，該方法對它們進行排序並分配以下百分位數：10%、20%、30%、40%、50%、60%、70%、80%、90%。

將 method 設定為“inclusive”用於描述總體資料或已知包含總體中最極端值的樣本。data 中的最小值被視為第 0 百分位數，最大值被視為第 100 百分位數。低於 m 個排序資料點中的第 i 個的總體部分計算為 (i - 1) / (m - 1)。給定 11 個樣本值，該方法對它們進行排序並分配以下百分位數：0%、10%、20%、30%、40%、50%、60%、70%、80%、90%、100%。

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

在 3.8 版本加入。

3.13 版本中的更改: 不再對僅包含一個數據點的輸入引發異常。這允許一次構建一個樣本點的分位數估計，並隨著每個新資料點逐漸變得更精確。

statistics.covariance(x, y, /)

返回兩個輸入 x 和 y 的樣本協方差。協方差是衡量兩個輸入的聯合變異性的指標。

兩個輸入必須長度相同（不少於兩個），否則會引發 StatisticsError。

示例：

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

在 3.10 版本加入。

statistics.correlation(x, y, /, *, method='linear')

返回兩個輸入的皮爾遜相關係數。皮爾遜相關係數 r 取值在 -1 到 +1 之間。它衡量線性關係的強度和方向。

如果 method 是“ranked”，則計算兩個輸入的斯皮爾曼等級相關係數。資料被替換為等級。相同的數值取平均等級。結果係數衡量單調關係的強度。

斯皮爾曼相關係數適用於序數資料或不符合皮爾遜相關係數線性比例要求的連續資料。

兩個輸入必須長度相同（不少於兩個），並且不必是常數，否則會引發 StatisticsError。

與開普勒行星運動定律相關的示例

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

在 3.10 版本加入。

3.12 版本中的更改: 添加了對斯皮爾曼等級相關係數的支援。

statistics.linear_regression(x, y, /, *, proportional=False)

返回使用普通最小二乘法估計的簡單線性迴歸引數的斜率和截距。簡單線性迴歸用以下線性函式描述自變數 x 和因變數 y 之間的關係：

y = 斜率 * x + 截距 + 噪聲

其中 slope 和 intercept 是估計的迴歸引數，noise 代表線性迴歸未解釋的資料變異性（它等於因變數的預測值和實際值之間的差異）。

兩個輸入必須長度相同（不少於兩個），且自變數 x 不能是常數；否則會引發 StatisticsError。

例如，我們可以使用Monty Python 電影的上映日期來預測假設他們保持相同速度到 2019 年 Monty Python 電影的累計數量。

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

如果 proportional 為真，則假定自變數 x 和因變數 y 成正比。資料擬合通過原點的直線。由於 intercept 總是 0.0，因此底層線性函式簡化為：

y = 斜率 * x + 噪聲

繼續 correlation() 的示例，我們來看看基於主行星的模型能多好地預測矮行星的軌道距離。

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

在 3.10 版本加入。

3.11 版本中的更改: 添加了對 proportional 的支援。

異常

定義了一個異常。

exception statistics.StatisticsError

統計相關異常的 ValueError 子類。

NormalDist 物件

NormalDist 是一個用於建立和操作隨機變數正態分佈的工具。它是一個將資料測量的均值和標準差視為單個實體的類。

正態分佈源於中心極限定理，並在統計學中有廣泛應用。

class statistics.NormalDist(mu=0.0, sigma=1.0)

返回一個新的 NormalDist 物件，其中 mu 表示算術平均值，sigma 表示標準差。

如果 sigma 為負，則引發 StatisticsError。

mean

正態分佈算術平均值的只讀屬性。

median

正態分佈中位數的只讀屬性。

mode

正態分佈眾數的只讀屬性。

stdev

正態分佈標準差的只讀屬性。

variance

正態分佈方差的只讀屬性。等於標準差的平方。

classmethod from_samples(data)

建立一個正態分佈例項，其 mu 和 sigma 引數透過 fmean() 和 stdev() 從 data 估計。

data 可以是任何 可迭代物件，並且應該包含可以轉換為 float 型別的值。如果 data 不包含至少兩個元素，則引發 StatisticsError，因為估計中心值至少需要一個點，估計離散度至少需要兩個點。

samples(n, *, seed=None)

為給定的均值和標準差生成 n 個隨機樣本。返回一個 list 浮點值。

如果給定 seed，則建立底層隨機數生成器的新例項。這對於生成可重現的結果很有用，即使在多執行緒環境中也是如此。

3.13 版本中的更改。

切換到更快的演算法。要重現以前版本的樣本，請使用 random.seed() 和 random.gauss()。

pdf(x)

使用機率密度函式 (pdf)，計算隨機變數 X 接近給定值 x 的相對可能性。在數學上，它是當 dx 趨近於零時，比率 P(x <= X < x+dx) / dx 的極限。

相對可能性被計算為樣本出現在狹窄範圍內的機率除以該範圍的寬度（因此稱為“密度”）。由於可能性是相對於其他點而言的，因此其值可以大於 1.0。

cdf(x)

使用累積分佈函式 (cdf)，計算隨機變數 X 小於或等於 x 的機率。在數學上，它表示為 P(X <= x)。

inv_cdf(p)

計算逆累積分佈函式，也稱為分位數函式或百分點函式。在數學上，它表示為 x : P(X <= x) = p。

找到隨機變數 X 的值 x，使得變數小於或等於該值的機率等於給定機率 p。

overlap(other)

衡量兩個正態機率分佈之間的一致性。返回一個介於 0.0 和 1.0 之間的值，表示兩個機率密度函式的重疊面積。

quantiles(n=4)

將正態分佈分成 n 個等機率的連續區間。返回一個由 (n - 1) 個分隔這些區間的切點組成的列表。

將 n 設定為 4 表示四分位數（預設）。將 n 設定為 10 表示十分位數。將 n 設定為 100 表示百分位數，它提供 99 個切點，將正態分佈分成 100 個大小相等的組。

zscore(x)

計算描述 x 的標準分數，即 x 偏離正態分佈均值的標準差數量：(x - mean) / stdev。

在 3.9 版本中新增。

NormalDist 的例項支援與常數的加法、減法、乘法和除法。這些操作用於平移和縮放。例如：

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

不支援用常數除以 NormalDist 的例項，因為結果將不是正態分佈。

由於正態分佈源於獨立變數的加性效應，因此可以加減兩個獨立正態分佈的隨機變數，這些變量表示為 NormalDist 的例項。例如：

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

在 3.8 版本加入。

示例與技巧

經典機率問題

NormalDist 輕鬆解決經典機率問題。

例如，給定SAT 考試的歷史資料，顯示分數呈正態分佈，平均值為 1060，標準差為 195，計算分數在 1100 到 1200 之間的學生百分比，四捨五入到最接近的整數。

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

找出 SAT 分數的四分位數和十分位數。

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

蒙特卡羅模擬的輸入

為了估計難以進行分析求解的模型的分佈，NormalDist 可以為蒙特卡羅模擬生成輸入樣本。

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

近似二項式分佈

當樣本量很大且成功試驗的機率接近 50% 時，正態分佈可用於近似二項式分佈。

例如，一個開源會議有 750 名參會者，兩個會議室的容量為 500 人。有一個關於 Python 的講座，另一個關於 Ruby 的講座。在之前的會議中，65% 的參會者更喜歡聽 Python 講座。假設人口偏好沒有改變，Python 會議室保持在其容量限制內的機率是多少？

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

樸素貝葉斯分類器

正態分佈通常出現在機器學習問題中。

維基百科上有一個關於樸素貝葉斯分類器的很好的例子。挑戰在於根據身高、體重和腳尺寸等正態分佈特徵的測量結果來預測一個人的性別。

我們得到了一個包含八個人測量結果的訓練資料集。測量結果假定為正態分佈，因此我們使用 NormalDist 總結資料。

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

接下來，我們遇到一個新的人，其特徵測量結果已知，但性別未知。

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

從男性或女性 50% 的先驗機率開始，我們將後驗機率計算為先驗機率乘以給定性別的特徵測量結果似然的乘積。

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

最終預測取最大的後驗機率。這稱為最大後驗估計或 MAP。

>>> 'male' if posterior_male > posterior_female else 'female'
'female'